みなさんこんにちは。
インスパイアの喜多です。

少し前ですがピタゴラスの定理と戯れる機会がありました。
かなり限定的なケースなので恐らくみなさんの参考になることはないと思うのですが、
とっても懐かしい気持ちになったので紹介させていただきます。

やらないといけなかったこと

〇円形のコンテンツ内にピッタリ収まるようスクロールボックスを設置

決まっていること

〇カスタム投稿により円の大きさ、円の色、円の中に入る文章が自由に入力可能
〇ボックスは border-radius: 50%; で円形にされており、そのボックス内に文章が格納される
〇ボックス（円の大きさ）は数値指定で様々な大きさに指定可能（下限上限あり）で、モニタサイズによっても可変
〇中に入る文章も文字数制限なし
〇円の中に入る文章ボックスは正方形状で、円内めいっぱいの大きさにしたい。

やったこと

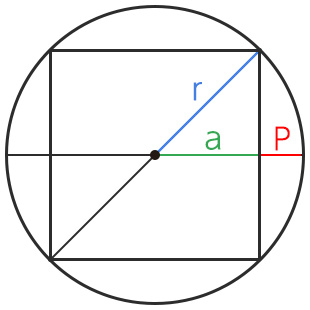
つまり円の中にこんな感じの正方形が出来るように調整する感じでした。
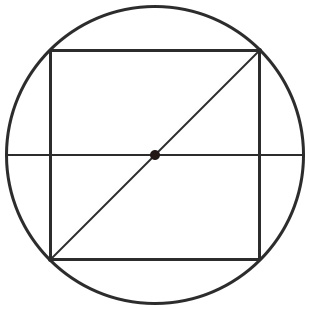今回は元のHTML記述をあまり変えてはいけないという縛りがあったので、
CSSであれやこれやをした形になります。

方法は様々あるようなのですが、
今回はHTML側の記述の都合でpaddingを用いた形式を採用しました。
下図の中のPを算出して、円形のボックスに padding: P; を指定します。

上記の条件通りであれば円の直径 = ボックスの横幅（width）になるので、

r = width / 2
P = r – a
a² + a² = r²

を解いていけばPが出てきます。
ただそれ以前に直角二等辺三角形の辺の比は「 1：1：√2 」というのがあるので、

a = r / √2
a = width / 2√2

あとは真ん中の式を使って

P = (width / 2) – (width / 2√2)
P = (2 – √2 ) / 4 * width

√2をだいたい1.414くらいとして考えれば、

P = 0.1464 * width

になります。
なのでそこまで精度を求めないのであれば、

padding : 15%;

を入れておくだけでいい感じですね。結果だけ見ればすごくシンプルです。
あとは出来るだけ隙間なく詰めていきたいのであれば、14.6%, 14.64%, 14.645%, 14.6447%と小数点を詰めていけばいい感じですね。

なんかここまでシンプルな結果に落ち着くと、
私自身が無知なだけで実はこんなのみんな当たり前に知ってるとかありそうで怖いんですけどそんなことないですよね？
義務教育は受けたつもりなのですが、まやかしだった可能性も否定できません。

ただ、こんなことを言ってしまうと元も子もないのですが、
上で言ったような円の中に padding : 15%;  を指定して正方形のスペースを作るようなデザイン、今後ほかで使うかといわれると正直何とも言えないんですよね。
応用できる場面があるといいのですが。

この部分もまた時間があるときにでも、可能性を追求してみたいと思います。
それでは、また。

P.S

この間いい感じの火加減の鶏チャーシューを作ることができたのですが、
食べてしばらく腹痛が止まりませんでした。
封印です。